Lift a rock in your garden and you might find a linear regression model. They are everywhere, working hard to predict all sorts of things, like how much further you can drive with this much fuel in the tank, or how much your house might sell for in your neighborhood. Linear regression models owe their success to their ease-of-use as well as their natural interpretability – most people would probably find it a lot harder to predict the output of a neural network, compared with that of $y=2x$.

Unfortunately, it is this ease-of-use and interpretability that make linear regression models especially prone to misuse, even by people who should know better¹. Before rushing to apply a model (any model), we need to ask ourselves two questions:

1. What does this model assume?
2. Do these assumptions make sense for our data?

As it turns out, the linear regression model makes some pretty strong assumptions that don’t always hold up in reality. This writeup takes a look at these assumptions, what happens when they don’t hold, and which ones we can bend.

Table of Contents

Simple linear regression

The goal of a linear regression model is to model $k$ response variables, $Y_{1},Y_{2},…,Y_{k}$ using $p$ predictor variables, $X_{1},X_{2},…,X_{p}$. In this article we will focus on “simple linear regression”, or SLR $(k=1)$ to avoid getting bogged down in notation. To model our response $Y$ using $p=3$ predictor variables, for example, we assume a relationship of the form

$$ Y = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \beta_{3}X_{3}, $$

where $\beta_{i}$ are predictor coefficients that have been found by the end of the fitting process.

Most of the core assumptions underlying linear regression have to do with the residuals, which are used to estimate prediction errors. Since they play such an important role in the modeling process, it’s worth taking some time to formally introduce them.

Meet the residual

To train a model, you need data. More specifically, you need a set of $N > p$ response observations and predictor measurements, ${(\hat{y_{i}}, x_{i1},x_{i2},x_{i3} )}_{i=1}^{N}$. Note the little hat sitting on $\hat{y_i}$. Our model formulation assumes that each of our responses is corrupted by some error $\epsilon$ such that for our $i$th observation, $\hat{y_i} = y_i + \epsilon_i$. The hat indicates that the observations $\hat{y_i}$ are actually estimates of the true responses $y_i$ that we can never observe.

Our SLR model relates the predictor measurements to the observations by

$$ \hat{y_i} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{i1} + \hat{\beta_{2}}x_{i2} + \hat{\beta_{3}}x_{i3} + \epsilon_{i}, $$

with our fitting process giving us estimates $\hat{\beta_i}$ of the true, hidden coefficients $\beta_i$. Our model thus consists of a deterministic component (i.e., the equation for $Y$ in terms of the $X_i$s) and a random component, represented by the error $\epsilon$.

Since there is no way to know the true response, we can never know the error terms $\epsilon_i$. So we estimate them using residuals. Compared directly,

• the error $\epsilon_i$ is the difference between the measured value and the (unobservable) true value,

$$\epsilon_i = y_i - y,$$

• the residual $r_i$ is the difference between the measured value and the predicted value computed from the model,

$$r_i = y_i - \hat{y_i}.$$

Now that we have some measure of prediction error in the residuals, we can use them to build a loss function that describes the overall model error. Linear regression then works to find the coefficient values that minimize this loss function. The L2-norm loss function $L = \sum_{i=1}^{N}r_i ^2$ is popular because it punishes outliers and makes finding the optimal coefficients a matter of plugging values into a formula.

Out with the assumptions

Although you will see all sorts of assumptions scattered throughout this article, there are four major ones (each with their own subsection) that rule them all. That is, these four alone are sufficient for linear regression analysis. Some are less demanding than others. Ultimately, you can probably get away with bending all of them in some way (as long as the statisticians aren’t looking), with the caveat that your model may become unreliable and therefore unsuitable for inference. Let’s see what can happen.

Normality

Our first assumption is inherent in the name of the model: the response is a linear combination of the predictors. This supposedly fundamental assumption is arguably the one that gets overlooked most of the time. Why? In a nutshell, when you’re close enough to a curve, it looks like a straight line.

There’s a reason the “flat Earth” theory was so compelling before NASA.

In practice, we have some wiggle room with this one. As long as our response data $y_{i}$ are far away from any theoretical limit, we can generally draw a straight line through the data and that will be enough for all sorts of applications. CEOs can project their yearly sales, consumers can work out their monthly electricity consumption, and life goes on.

On the other hand, if we are looking to describe phenomena more generally, then we need to take the idea of linearity more seriously. Let’s say you want to build an SLR model to describe height $H = \beta_{0} + \beta_{1}W$ as a function of weight $W$, using data from your coworkers. As long as you have enough coworkers (and enough of them agree to give you that data), you will end up with coefficients $\hat{\beta_{i}}$ that capture this relationship for adults that more or less resemble your coworkers. That last point is crucial. If you are a professional wrestler (presumably learning statistical analysis in your own time) and each of your coworkers resembles Thanos, your coefficients will be useless for predicting the height of an average human being. If your coworkers are a regular group of men and women, your coefficients won’t help you to predict the height of a child. In general, the more useful you want your model to be, the less likely you’ll be using linear regression.

The bottom line is that under certain circumstances, an SLR model might be enough to describe non-linear phenomena. If you scatter your data and it looks like they will conform to a straight line without excluding too many outliers, it might be all you need. Just be wary about using the model to extrapolate data beyond your current range of responses.

Independent errors

To assess how good our model is, and to do it correctly, we need the residuals to have properties that are like the actual errors they are supposed to estimate: independent and normally distributed, with zero mean and fixed variance. Each of the remaining core assumptions behind linear regression is right there in that last sentence.

What does it mean for the residuals to be independent? This means that they should not have a relationship with any of the predictors, or each other. When we plot the residuals as a function of a predictor variable (or as a function of time, for time-series data), we don’t want to see any kind of pattern. Nothing except some random-looking points centered on zero. Anything else means that the residuals have some kind of structure, suggesting that the model might not be a great fit for the data.

To see what it means when we don’t have independent residuals, we’ll use the Boston Housing dataset to build a (naive) SLR model of the median house value $V$ based on a single predictor, the mean number of rooms in a house $RM$, related by $V = \beta_0 + \beta_1 RM$. We fit our model and sure enough, the more rooms in your house, the greater its predicted value (Fig. 2, left panel). No surprises there.

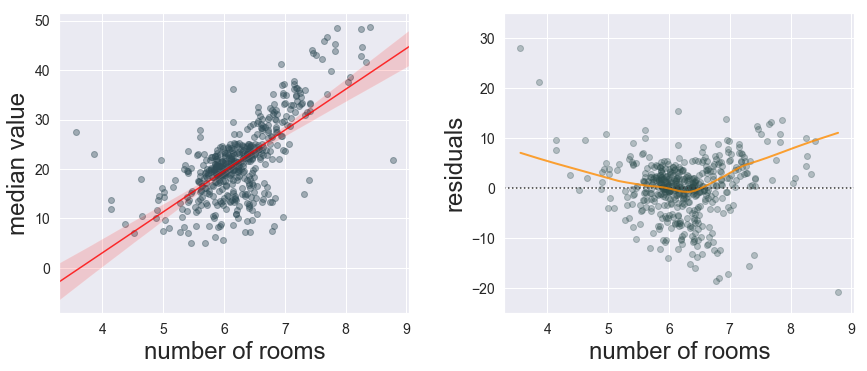
Taking a look at the residual plot in Fig. 2B (right panel), we see that the residuals start off with a positive bias, sagging in the middle of our response range, before increasing again for large room counts. We are underestimating value for houses that don’t have an “average” number of rooms.

This residual plot is telling us that our model’s deterministic component (i.e., the formula $V = \beta_0 + \beta_1 RM$) is missing something important. But before we try adding other predictors, let’s make a small change to our single predictor and use its square $RM^2$, as suggested by the authors of the study that initially made use of this dataset². This cheap modification gets us a slightly better r-squared value (from 0.47 to 0.50) as well as a residual plot that bends a bit closer to zero (Fig. 3). Transforming the predictors (or the response) can improve the distribution of our residuals and the model’s fit quality.

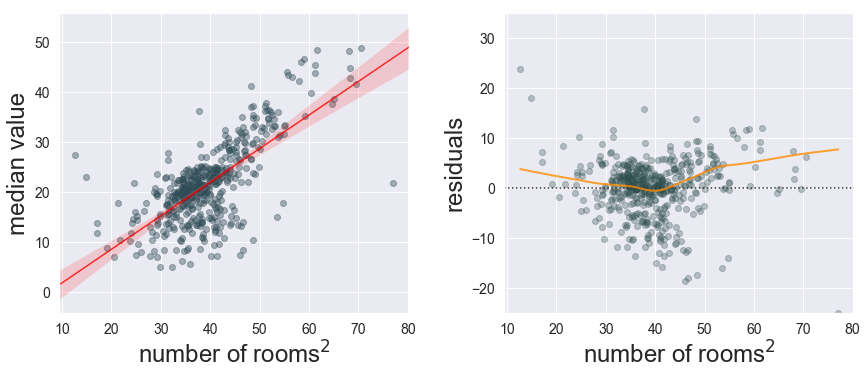
Of course, it’s unlikely that we can model something as complex as house value with a single predictor. By including two more predictors (house age and per-capita crime), we easily improve the model fit ($R^2=0.65$) and our residuals tend closer to zero. Generally, additional predictors should be considered if (a) they are informative for the response variable, and (b) they are (at most) weakly correlated with any of the existing predictors.

Correlation, whether among the residuals or among the predictors, can cause all sorts of problems in regression analysis. As an extreme example, consider what would happen if we fit a model of house value with two perfectly correlated predictors, $RM$ and $RM^2$. Compared with the model that only includes $RM^2$, we net ourselves an artificial boost in $R^2$ (from 0.50 to 0.53) and our $RM^2$ coefficient estimate ends up being an order of magnitude larger (from 0.67 to 2.23). Not only do we not gain any meaningful insight with our extra predictor, we actually lose insight – we have made it harder to understand the true effect of room count on house value.

Linear regression has a couple more things to say about the distribution of our residuals.

Normally-distributed errors

The errors (and the residuals) should not only have a mean of zero, they should also be normally distributed with constant variance $\sigma^2$. We can write this as

$$ \epsilon_i \sim \textrm{Normal}(0,\sigma^2). $$

If the errors are not normally distributed, you can still go ahead and compute coefficients, but your measures of uncertainty and significance testing may be compromised if you don’t have enough observations. For instance, the standard error terms for the predictor coefficients and the model itself, and by extension, their associated confidence intervals, are all computed under the assumption of residual normality. If you do find evidence of non-normality (preferrably through statistical measures like the Kolmogorov-Smirnov test, rather than by visual inspection), but you’ve decided that it’s acceptable, it might be best to use wider confidence intervals to indicate this additional uncertainty, documenting your rationale.

Your ears might have detected a loophole earlier, in that we might not need normally-distributed residuals if our observation count is high enough. Thanks to the central limit theorem, it turns out that with a moderate observation count (let’s say $N>20$), linear regression will be perfectly capable of handling your non-normal response data³. The specific number of observations you need will vary depending on whether your response variable is “well-behaved” or not. If you are dealing with extremely skewed response distributions or large outlier counts, for instance, you will likely need (many) more observations.

Homoscedasticity

In the last section we described the errors as being normally distributed, but we didn’t talk about their variance. When we write $ \epsilon_i \sim \textrm{Normal}(0,\sigma^2),$ we are saying that the errors are identically distributed for every observation $i$, as if each is being drawn from the same normal distribution with zero mean and variance $\sigma^2$. The errors are said to be homoscedastic.

(Which is a bit of a mouthful. I’d rather just say they have constant variance.)

We can test for constant variance using most modern statistical libraries (e.g. statsmodels) but a quick visual indication can be found in the residual plots. If the spread of residuals appears to vary with a given predictor, you should probably run a test to confirm its severity and whether you can tolerate it in your analysis. Too much variability will compromise any measures of uncertainty or significance.

All too human

So with all these statistical landmines, why are linear regression models so pervasive? Probably because we can understand them. It is difficult to wrap our minds around nonlinear phenomena because the mental models we use to make sense of our world tend to be linear!